Gottfried Wilhelm Leibniz
I. Intro
Gottfried Wilhelm von Leibniz was the definition of a polymath. He was a prolific thinker whose ideas covered not only philosophy but mathematics, physics, biology, politics, medicine, religion, technology, and language. Some historians have dubbed him “the last universal genius” because of the sheer breadth of his thinking. He’s most famous for two things: his optimistic philosophical outlook, and his invention of calculus. But, with his wide interests and apparently limitless talent for scholarship, Leibniz rivaled ancient philosophers like Aristotle and Pythagoras. (Though some later philosophers, notably Kant, might object to Leibniz’s being labeled as the “last” such genius).
As early as 1672, Leibniz invented one of the first mechanical calculators, a device he called the “stepped reckoner.” It was a hand-cranked machine that could perform simple arithmetic – not unlike the basic calculator on a modern phone. Some philosophers have made the argument that this was the first step on the long road to the digital computer; whether or not that’s fair, it was certainly an impressive achievement for its time.
In politics, he was a keen observer of power and seems to have been fascinated by the grand chess game of international competition. His political acumen was greatly in demand at the time, when Europe was destabilized by war, religious strife, and the imbalance of power created by Louis XIV’s highly centralized monarchical rule. As a keen political maneuverer, Leibniz had opportunities to travel all over Europe and interact with elites in every field of art and science – all of which fueled his immense intellectual appetite.
II. Bio
Leibniz’s scholarly career started early. His father was a noted professor of moral philosophy who encouraged his son’s broad curiosity. When Leibniz was six, his father died and left him a vast library of works in Latin. The young philosopher suddenly had access to a huge range of ideas, and apparently he devoured them with enthusiasm. At 14 he entered the University of Leipzig, where his father had once taught, and after two years of study graduated with his bachelor’s degree. At 18 he earned a master’s degree and turned his attention to a career in law.
Leibniz could easily have pursued an academic career, but he seemed more interested in the law (perhaps because it was more lucrative, then as now). His legal and political work eventually got him sent to Paris, which at that point was the center of European science and philosophy, as well as the seat of Louis XIV, one of the continent’s most powerful monarchs. In Paris, Leibniz was exposed to state-of-the-art physics, and even though he had relatively little training in science he picked it up quickly. Soon, he was making major discoveries in his own right.
Leibniz’s most important discovery was an attempt to solve some major problems in physics – it was the mathematical language we now call calculus. Unfortunately, Leibniz wasn’t alone in his discovery of calculus. At exactly the same time, a young English prodigy named Isaac Newton was developing an almost identical mathematical system.
Leibniz was first to publish. In 1684, he published a paper that used calculus but didn’t explain its full implications. Three years later, in 1687, Newton published his Principia Mathematica, still recognized as one of the most important works in the history of science. Newton’s book also used a version of calculus.
At first, neither author realized the full implications of the other’s work. Only decades later, when Newton had become the titan of British science, did he claim that Leibniz had stolen his idea. Leibniz objected, arguing that he had arrived at calculus independently. Historians now generally agree that Leibniz was telling the truth, although it’s also true that Leibniz had a copy of some papers by Newton that might have at least spurred him along. But Newton had powerful supporters in the scientific and political worlds, and Leibniz became a controversial figure. He had a convivial nature and didn’t like being involved in these sorts of disputes (unlike Newton, who was more combative), and by the end of his life he had stopped trying to defend himself. Only later, in retrospect, would the scholarly community fully acknowledge Leibniz’s achievement.
III. Leibniz’s Ideas
a. The Best of All Possible Worlds
Leibniz’s outlook was profoundly optimistic. He argued that the we live in “the best of all possible worlds” – this in spite of the bloody conflicts that were tearing Europe apart even as he wrote. But Leibniz didn’t come up with this idea by shutting his eyes to the ugliness around him. Instead, he argued that any improvement to the world would either produce a logical contradiction or would lead to some worse outcome later on down the line.
As a rationalist, Leibniz favored logical deduction rather than empirical observation to support his arguments. In this case, he started from the basic principle that God is benevolent and all-powerful, and therefore would not (in fact, could not) choose to create a world with unnecessary suffering. He also assumed that God was rational and could not create a world with logical contradictions in it. Therefore, Leibniz argued, all suffering is necessary either for the logical consistency of the universe or for the greater benefit of all humans across time.
b. Calculus
Leibniz’s philosophy is unpopular with modern students, who tend to question its assumptions about the nature and existence of God. His most lasting contribution, in fact, was his invention of calculus (which is also unpopular with students, but for very different reasons).
In the 17th century, physicists had a problem. They didn’t have a mathematical language to describe their questions, and so didn’t have the tools to solve them. Algebra had been developed by Arabic and Indian scholars centuries earlier, and it was extremely useful for describing relationships between quantities. But the physical world isn’t just made up of relationships – it’s made up of processes that change those relationships, usually in a continuous or gradual way. You need a different kind of math to describe those changes.
Algebra, for example, can describe the relative strengths of two magnets and predict the attractive force between them at a given distance. But when the magnets move closer together, the forces involved will change and you need to describe a new relationship. In theory, of course, you could develop a different algebraic function for magnets at 1m, .5m, .25m, etc. And if you use 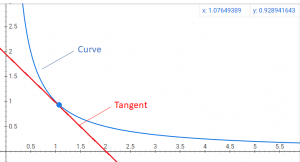
What Newton and Leibniz independently figured out was this: if the magnetic force can be described as a curve, then the change at any given point can be described by the slope of a tangent line at the corresponding point. By solving a problem of geometry in the description of tangent lines, calculus allows you to describe the physics of dynamic systems.
So what Newton and Leibniz discovered – independently and almost simultaneously – was that you could take a principle from algebra, mix it with some ideas from geometry, and use it to solve problems in physics.
IV. Controversies
Leibniz and Dr. Pangloss
It’s easy to imagine what some people thought of Leibniz’s optimistic outlook. Many later philosophers ridiculed the idea that we live in “the best of all possible worlds,” dismissing it as founded purely on emotional desires and self-deception rather than rationality or objective evidence.
The most effective critic was Voltaire, who made Leibniz a character in his satirical novel Candide. The story centers on a young man named Candide, who learns Leibnizian philosophy from his tutor, Dr. Pangloss. Pangloss trains Candide in the “best of all possible worlds” philosophy, which utterly fails to prepare the boy for the real world. As Candide witnesses war, ignorance, and suffering, he is slowly forced to give up his naïve acceptance of Leibniz’s optimism. Voltaire’s satire was so effective that we now have a word – panglossian – for someone who is delusionally optimistic and unable to accept that some things really aren’t for the best. Any philosophy resembling that of Leibniz can now, thanks to Voltaire, be described as panglossian.
In fact, the critique has extended out of philosophy and into biology, where the eminent scientist Stephen Jay Gould wrote a paper criticizing a mistaken view of evolution that he calls “the panglossian paradigm.” The panglossian paradigm is the view that evolution is driven by innate improvement rather than an interplay of reproduction with random genetic change. Gould points out that evolution often has random and even deleterious effects.
V. Quotes
Quote #1
“As there is an infinity of possible universes in the Mind of God, and as only one of them can exist, there must be a sufficient reason for God’s choice, which pushes him toward one over another. And this reason can be found only in the rightness, or the degrees of perfection, that these worlds contain.” (1714)
This is the most succinct statement of Leibniz’s argument for optimism. The underlined portion is the crux of the whole argument: since God is infinitely powerful and infinitely good, nothing constrains his choices other than pure rationality. That means when God chooses among all possible universes, he must choose the most perfect of all.
Quote #2
“I am convinced that the unwritten knowledge scattered among men of different callings surpasses in quantity and in importance anything we find in books.” (1688)
People often think of philosophers as loners, contemplating truth in great libraries or on the tops of mountains. And there’s some truth in that. But Leibniz was not one of those shut-in philosophers. He was a deeply social man who kept correspondence with thousands of friends throughout his life. As much as he loved reading and scholarship, his greatest pleasure came from good, stimulating conversation.
VI. In Pop Culture
The Pollyanna
Voltaire’s satire of Leibniz was so popular that “panglossian” characters became a pop-culture trope almost instantly. Today, we use the term “pollyanna” to describe a character who is just way too optimistic and maybe a little delusional. “Pollyanna” was originally the title of a 1913 coming-of-age novel about an optimistic little orphan girl who manages to put a positive spin on her difficult circumstances. The novel was made into several animated movies, most recently a 1989 Disney film. Examples are everywhere: in Frozen, for example, Elsa’s sister Anna takes a positive view on everything that happens – an approach that begins to fail her as circumstances get worse around her. (It’s possible that Anna was actually named after the “pollyanna” trope.) The main character from Parks & Recreation is another example. A lot of the comedy comes from her insistent positivity in spite of all evidence and reason.